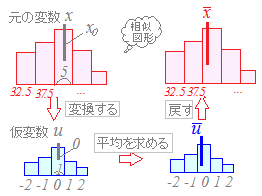
ヒストグラムから平均値を求める方法 私たちで、明るい時代にしていきましょうね さて!昨日は、平均値の考え方をお伝えしました。 詳しくは、こちらをご覧ください で、今日は、さっそくグラフから平均値を求めてみましょうか度数分布表の中央付近で,仮変数 0 にすると大きい方も小さい方も ±2 のように小さな整数値になって,計算が楽になるからです.先頭を 0 から始めて(仮平均を他の値に設定しても,例えば325としても)も正しく求めることはできますが,階級値の仮変数目的 画像中の輝度値のヒストグラム、平均・分散を求めた際の備忘録です コード 以下の画像のヒストグラム、平均・標準偏差を求めます lenapng テスト用の画像 blackpng 一様に真っ黒な画像
度数分布表から平均値 分散 標準偏差を求める
ヒストグラム 平均値 求め方
ヒストグラム 平均値 求め方-全体の平均値を下げる改善 あわせてバラツキを小さくする改善を 施すことが求められます ヒストグラムの平均値とバラツキでわかること ヒストグラムの平均値(ポジション) そしてバラツキの大きさ(幅) その規格との関係によって測定値の表し方 ヒストグラムによれば、測定値は平均値2728秒の近くの に集中しており、平均値から離れるに従って度数が減る。 式14と式16より、多数回の測定から式11を使って求めた平均値


中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su
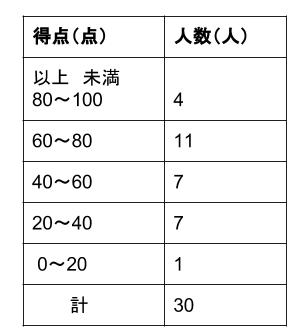
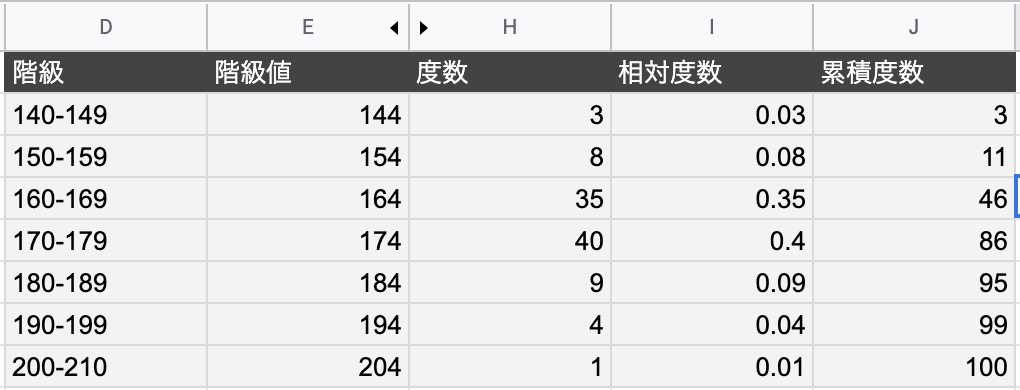
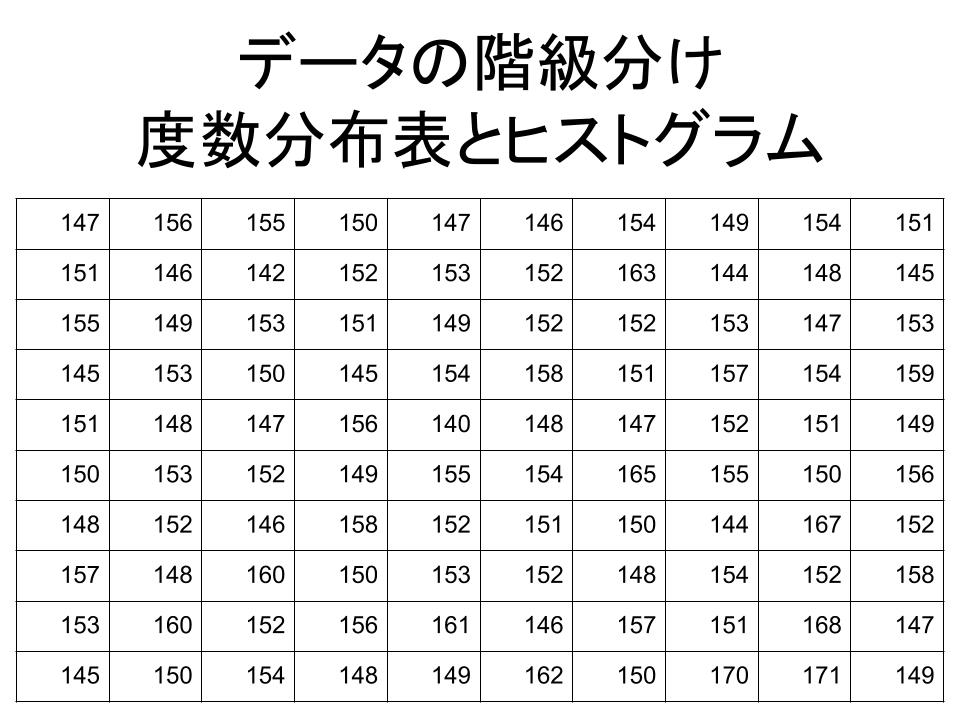
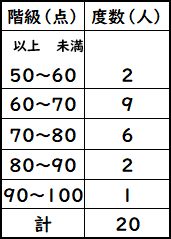
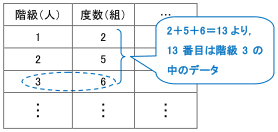
よって平均値は、\(\color{red}{268}\) となります。 次に中央値を求めます。 度数の合計が \(50\) と偶数なので、真ん中にくるデータは \(25\) 番目と \(26\) 番目ですね。ヒストグラムとは ヒストグラムとは画像処理以外の分野で使われることもあるが 画像処理の分野では、各濃度値に対してその濃度値を持った画素数を求めたもので、濃度ヒストグラム または単純にヒストグラムという。 ヒストグラムは主に横軸が濃度値、縦軸に画素数をとったグラフで表現かつて標準偏差の値をヒストグラムから計算したが、現今では標準偏差は Excel で簡単に求められ、その役目は終わった。 現在、ヒストグラムは、「分布の形」だけを診断の対象にしている(広がりや平均値は、 → 工程能力指数 Cpk で診断する)。
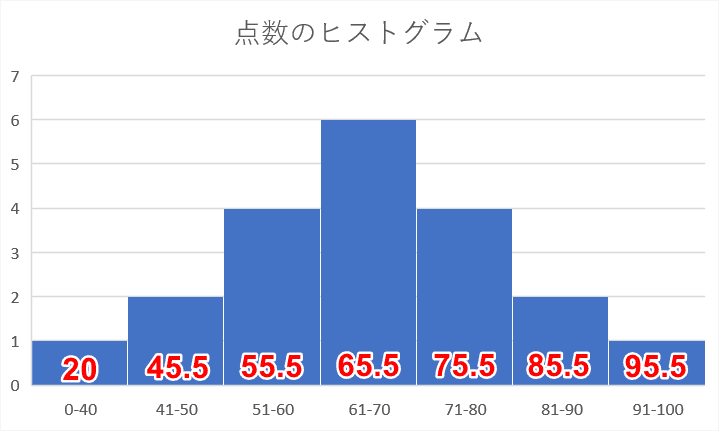
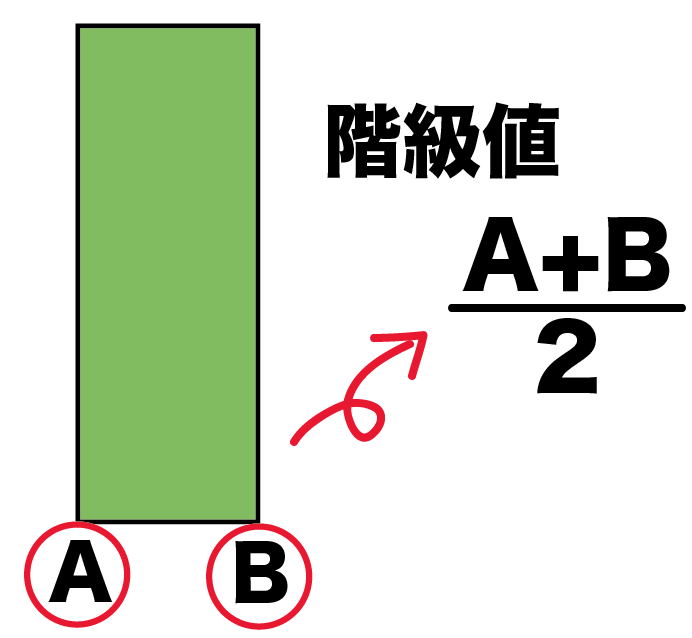
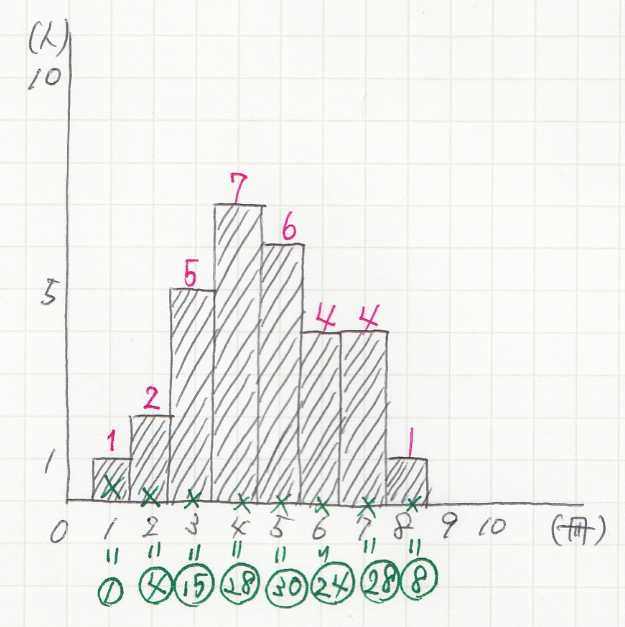
ヒストグラムから平均値を求められたね。 まとめ:ヒストグラムでも平均値ばっちこい ヒストグラムでも度数分布表でも大丈夫。 平均値の求め方は、 階級値×度数の合計 を 度数の合計 でわればいいんだ。 しっかり点をとっていこう。 そんじゃねー Ken目的 画像中の輝度値のヒストグラム、平均・分散を求めた際の備忘録です コード 以下の画像のヒストグラム、平均・標準偏差を求めます lenapng テスト用の画像 blackpng 一様に真っ黒な画像データの代表値 平均値 相対/度数のヒストグラムからの平均値の求め方 0 10 30 ¿ÈĹ(cm) ÅÙ¿ô(¿Í) ǵÌÚºä46(17¡Ý09?) 力学のりで k 個の質点の重心の座標xG = ∑k j∑=1 x jm j mj 力学 j 番目の質点の位置xj =階級値, 質量mj = fj そこを支えると
測定値の表し方 ヒストグラムによれば、測定値は平均値2728秒の近くの に集中しており、平均値から離れるに従って度数が減る。 式14と式16より、多数回の測定から式11を使って求めた平均値2 この項目で学ぶこと データの分布 =どのようなデータがどれぐらい出ているか =データがどのように広がっているか ヒストグラム データの頻度を可視化する 代表値 データ全体を分布中心のデータ1つで表す方法 平均値,中央値,最頻値 九州大学数理・データサイエンス教育研究センターヒストグラムから平均値を求める方法 私たちで、明るい時代にしていきましょうね さて!昨日は、平均値の考え方をお伝えしました。 詳しくは、こちらをご覧ください で、今日は、さっそくグラフから平均値を求めてみましょうか



度数分布表から平均値 分散 標準偏差を求める
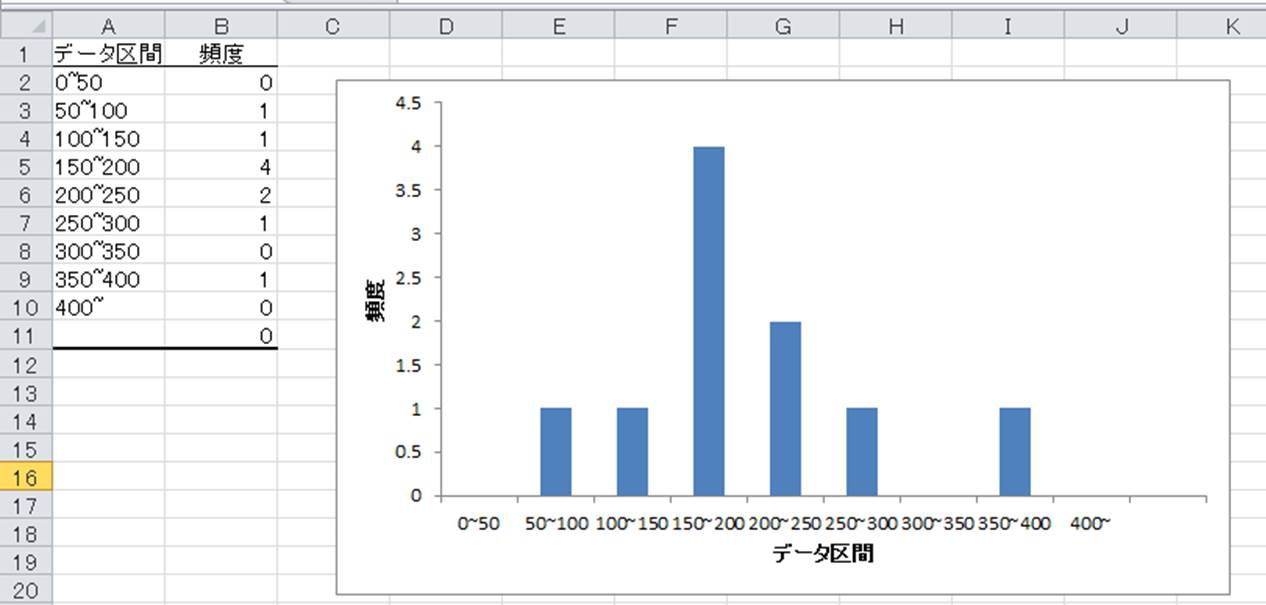


Excel エクセルで階級値を計算する方法
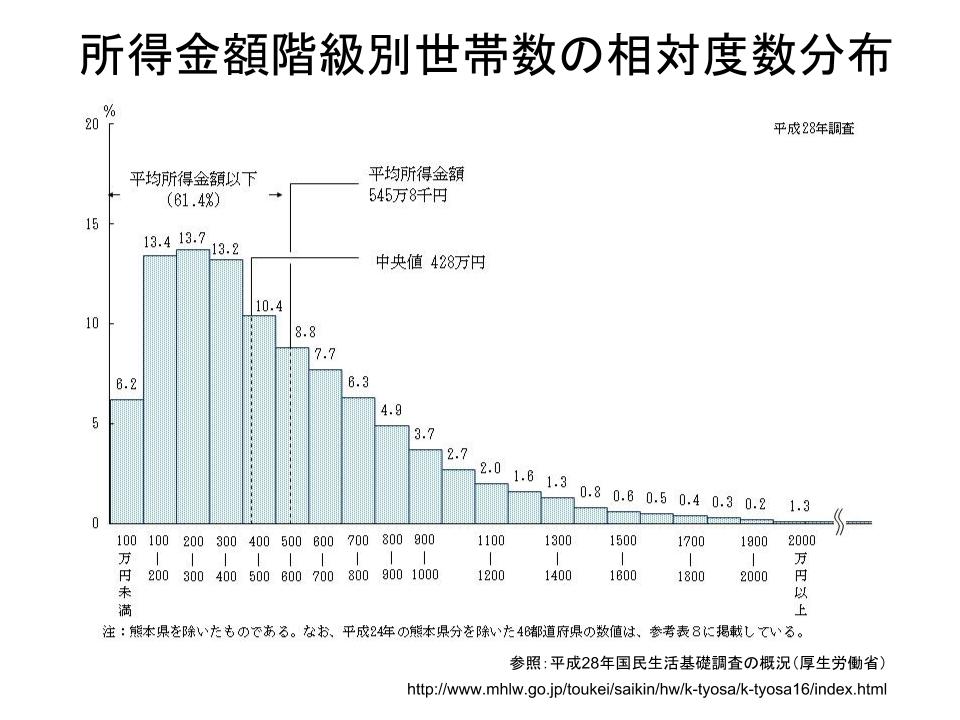
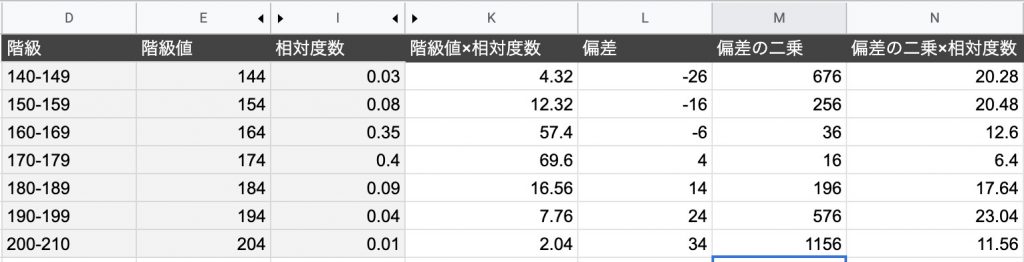
Skip to content Sobre nós;平均値(=average関数) 中央値(=median関数) 散布度(散らばり) 散 分 標準偏差 本日の内容 ばらつき具合とその指標 散布度の求め方 Zスコアと偏差値 使用するデータの特徴 代表値 代表値として「平均値」 を用いる 数学的に最も高度な代表値$$平均値=\frac{\sum{(階級値×世帯数)}}{\sum{世帯数}}$$ 計算すると、約1357という数字になるはずです。 試してみて下さい 階級値から標準偏差を求めよう 次に標準偏差を求めます。 まずは、偏差を求めます。 各偏差は $$偏差=階級値平均値$$ です。



ヒストグラムから階級値を使って平均値と標準偏差を求めよう シグマアイ 仕事で使える統計を


中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ
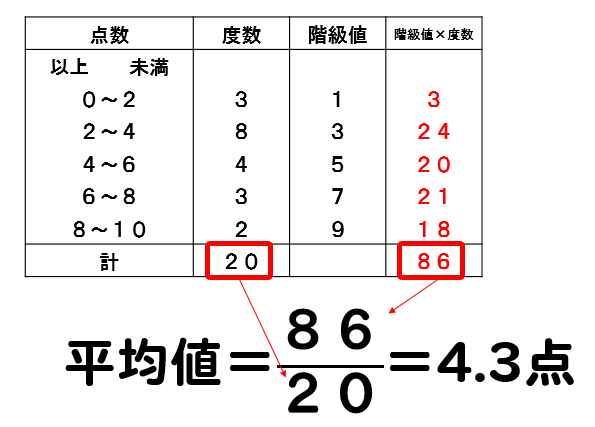
ヒストグラムとは ヒストグラムとは画像処理以外の分野で使われることもあるが 画像処理の分野では、各濃度値に対してその濃度値を持った画素数を求めたもので、濃度ヒストグラム または単純にヒストグラムという。 ヒストグラムは主に横軸が濃度値、縦軸に画素数をとったグラフで表現平均21÷64(総数)= ≒ 342 分 平均値342 分 ※平均値が割り切れないときは、四捨五入することが多い。(問題文の指示に従う) ※資料が度数分布表の場合は、求め方が違う。 (それぞれの階級値)×(度数)をすべて求め、その値を加える。参考 統計web 平均・中央値・モード;



ヒストグラムの平均値と標準偏差 階級値を使って推測しよう 度数分布表だけでok Youtube
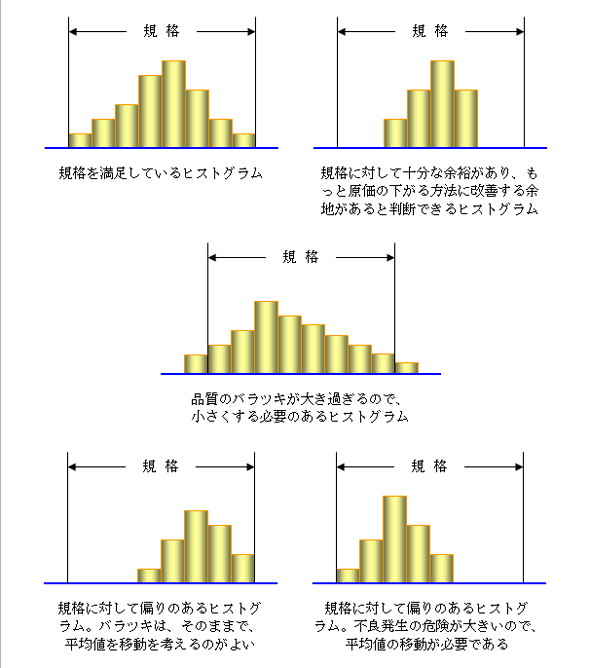


ヒストグラムの読み方 コツと経験則 実践 Ie 現場視点の品質管理 12 1 4 ページ Monoist
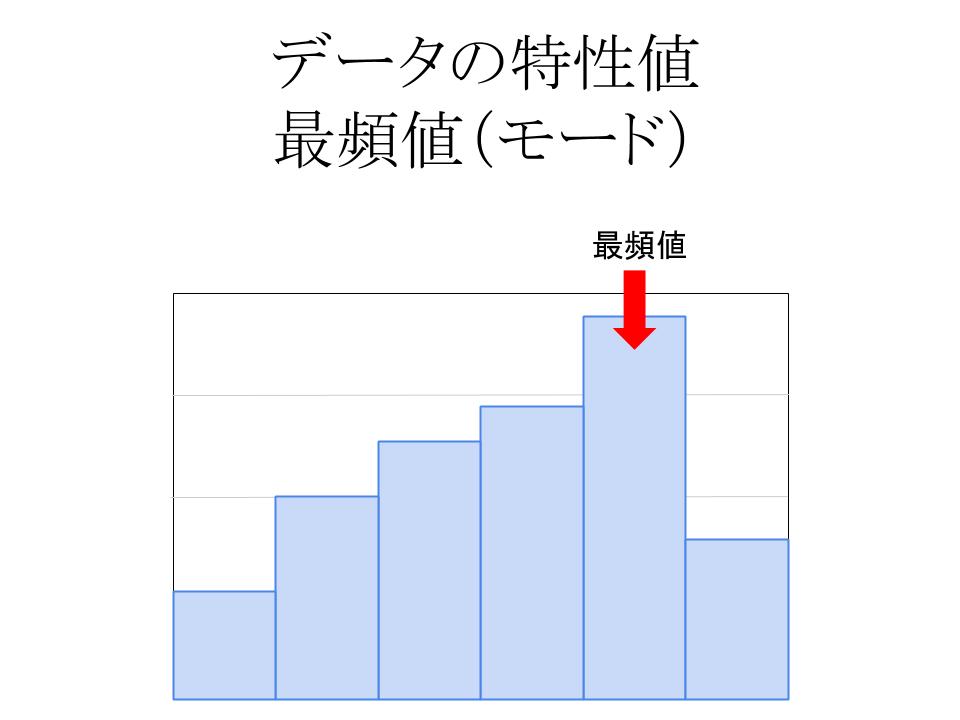
全体の平均値を下げる改善 あわせてバラツキを小さくする改善を 施すことが求められます ヒストグラムの平均値とバラツキでわかること ヒストグラムの平均値(ポジション) そしてバラツキの大きさ(幅) その規格との関係によって値の範囲はどちらも1~255です。 本ライブラリーでは高速化のために、分割された領域の平均値と標準偏差値の比較によっ て領域の再統合を行っています。 領域間の平均値、標準偏差値の差がそれぞれmatch_avr、match_stddev未満だと領域統合ばヒストグラムの高さ3 分の1となる理由を考えさせて,グラフに表現させる。 ② 度数分布表から中央値・最頻値を算出させる。(既習事項。電卓を使用。平均値は桁数が多くなり,電 卓では計算が困難なので,求め方のみ確認し,与えることとする。



度数分布表から相対度数を求める 苦手な数学を簡単に



正規分布と管理図 統計の基礎知識4 ものづくり まちづくり Btob情報サイト Tech Note
ヒストグラム(度数分布表)とは QC七つ道具 横軸に特性値を,縦軸に度数を目盛って区間の幅で柱状の図を書いた度数図を,一般にヒストグラム(histogram)と呼んでいる。 これを規格値と照合したりして,その製品の品質の状態が満足なものであるかどうかを判断するのに役立つ。全体の平均値を下げる改善 あわせてバラツキを小さくする改善を 施すことが求められます ヒストグラムの平均値とバラツキでわかること ヒストグラムの平均値(ポジション) そしてバラツキの大きさ(幅) その規格との関係によって参考 統計web 平均・中央値・モード;
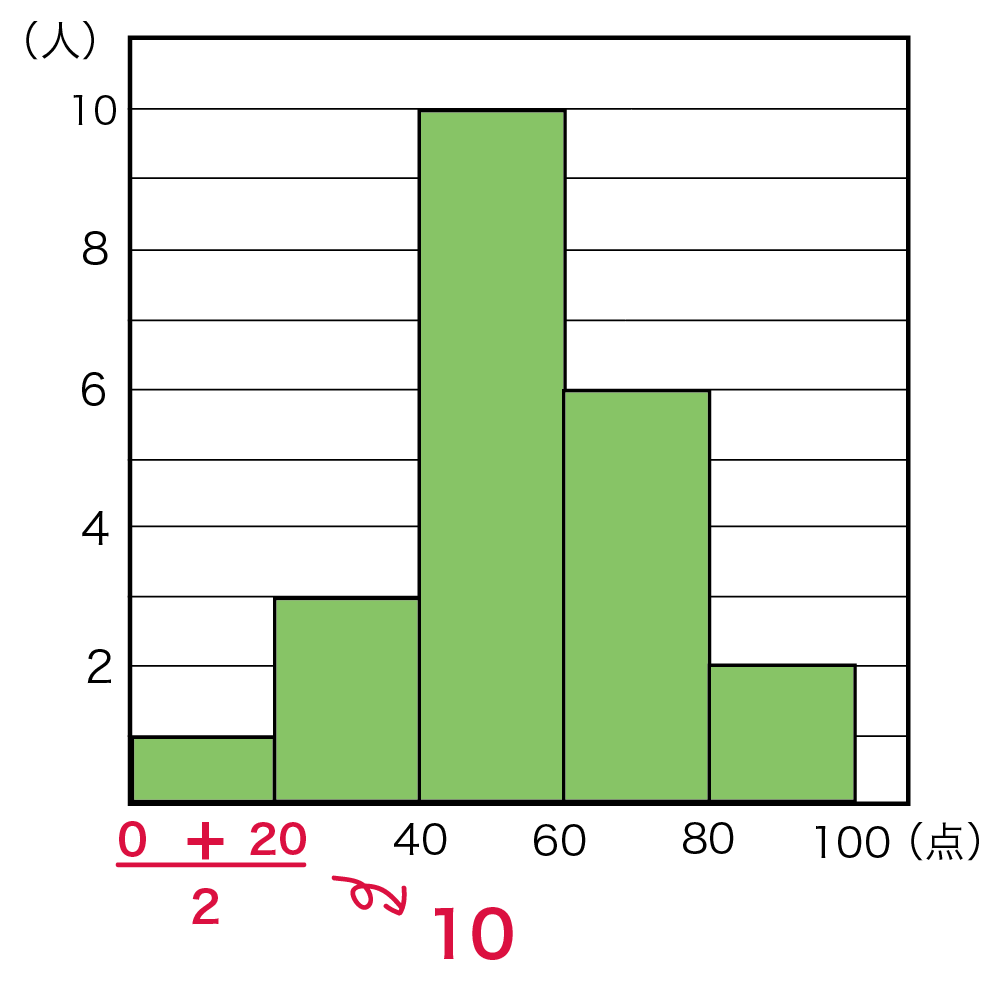


ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく
かつて標準偏差の値をヒストグラムから計算したが、現今では標準偏差は Excel で簡単に求められ、その役目は終わった。 現在、ヒストグラムは、「分布の形」だけを診断の対象にしている(広がりや平均値は、 → 工程能力指数 Cpk で診断する)。解き方 (階級値)×(度数)は次のようになる。 平均値= {(階級値)×(度数)}の合計 度数の合計 = 960 =48 (cm) 答 48 cm 考え方 45 cm 以上 50 cm 未満の階級値 47 5 cm を仮の平均とする。 平均値=仮の平均+ {(階級値-仮の平均)×(度数)}の合計ヒストグラムとは ヒストグラムはQC7つ道具のひとつで, 計量値(量的なデータ例 kg, m, L, Paなど単位のあるもの)の度数分布を棒グラフで表したものです度数を表した長方形(柱)を並べることで, 分布の形を可視化することができます
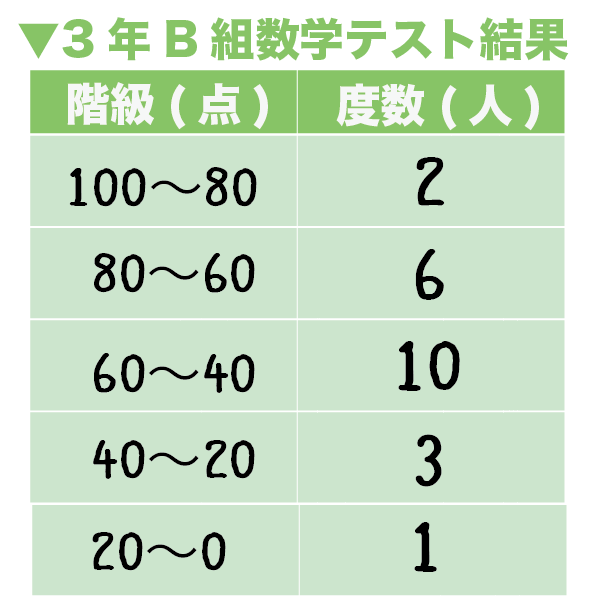


平均値 Japaneseclass Jp
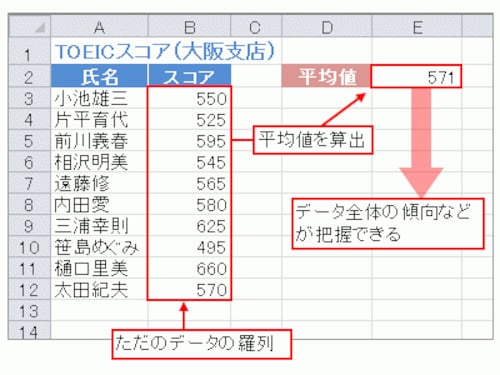


Excelで平均値 中央値 最頻値を算出する方法 エクセル Excel の使い方 All About
ばヒストグラムの高さ3 分の1となる理由を考えさせて,グラフに表現させる。 ② 度数分布表から中央値・最頻値を算出させる。(既習事項。電卓を使用。平均値は桁数が多くなり,電 卓では計算が困難なので,求め方のみ確認し,与えることとする。


3 2 平均 中央値 モードの関係 統計学の時間 統計web


T Sj Rtibkgobm


経営を学ぶ 経営学 Mba 起業



資料のちらばりと代表値 度数分布表からの平均値の求め方 中学数学 定期テスト対策サイト


度数分布表から標準偏差を求める 中卒でも分かる統計学入門 プログラマーを目指す 中卒 男のブログ


経営を学ぶ 経営学 Mba 起業


3 3 平均 中央値 モードの使い方 統計学の時間 統計web
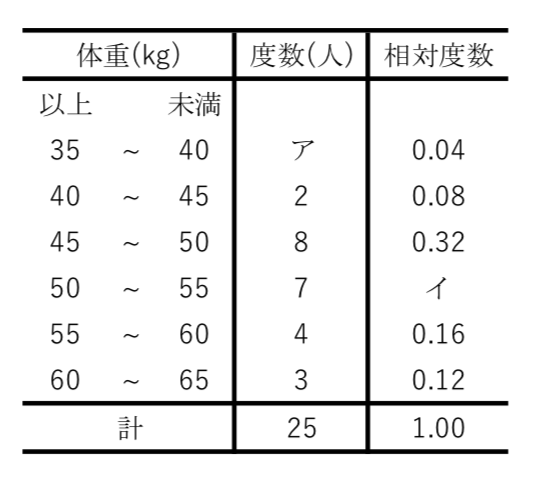


度数分布表を完成させよう 求め方は決まっている 苦手な数学を簡単に
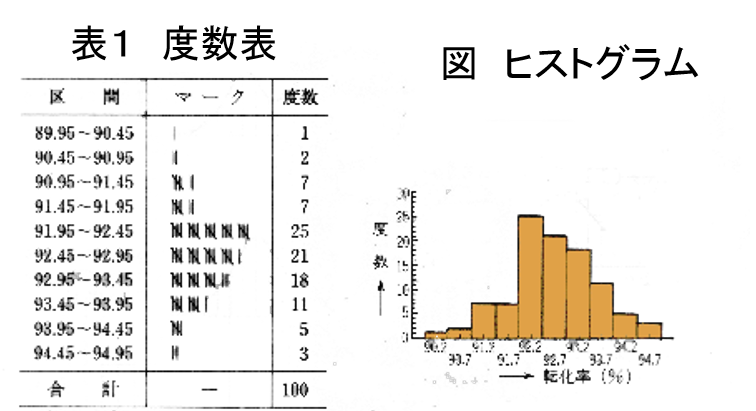


ヒストグラム 度数分布表 とは Qc七つ道具エクセル ヒストグラム 度数分布表 作成の方法 図解 日本のものづくり 品質管理 生産管理 設備保全の解説 匠の知恵



度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典


ヒストグラムの平均値の求め方教えて下さい ヒストグラムから Yahoo 知恵袋
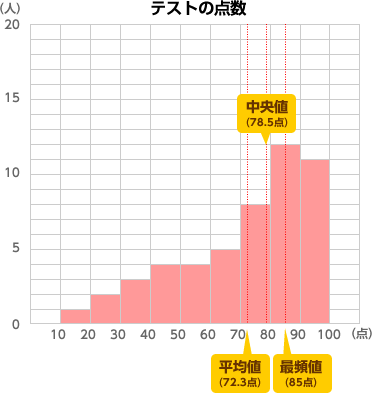


まなぼう統計 統計を知ろう 学ぼう データの特徴 変化をとらえよう 資料のちらばりを表す 代表値



中学数学 最頻値 モード の求め方がわかる2ステップ Qikeru 学びを楽しくわかりやすく



この問題の解説をお願いします Clear
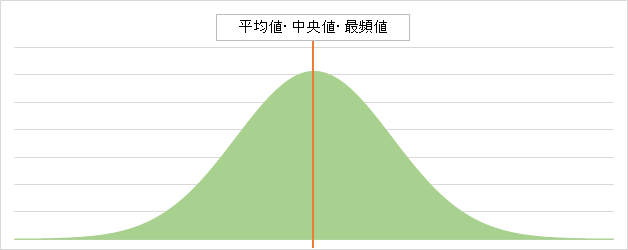


平均値 中央値 最頻値の違いをグラフのどこに位置するかで理解しよう 統計学が わかった



10分でヒストグラムと正規分布カーブを描く方法


3 5 歪度と尖度 統計学の時間 統計web
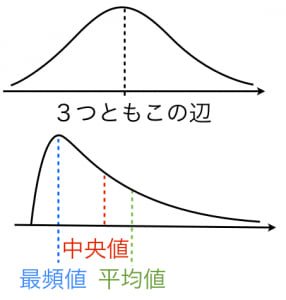


平均値 中央値 最頻値の求め方といくつかの例 高校数学の美しい物語
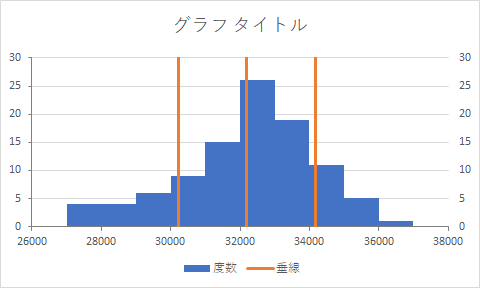


Excelによるヒストグラム 作図のためのtips 平均 規格値などの垂線を重ねる


経営を学ぶ 経営学 Mba 起業
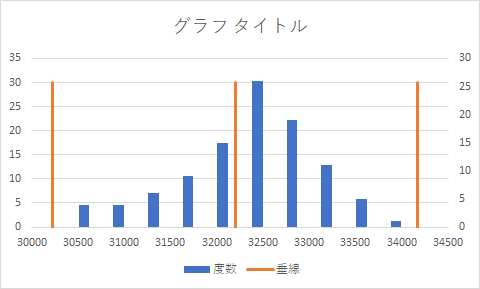


Excelによるヒストグラム 作図のためのtips 平均 規格値などの垂線を重ねる
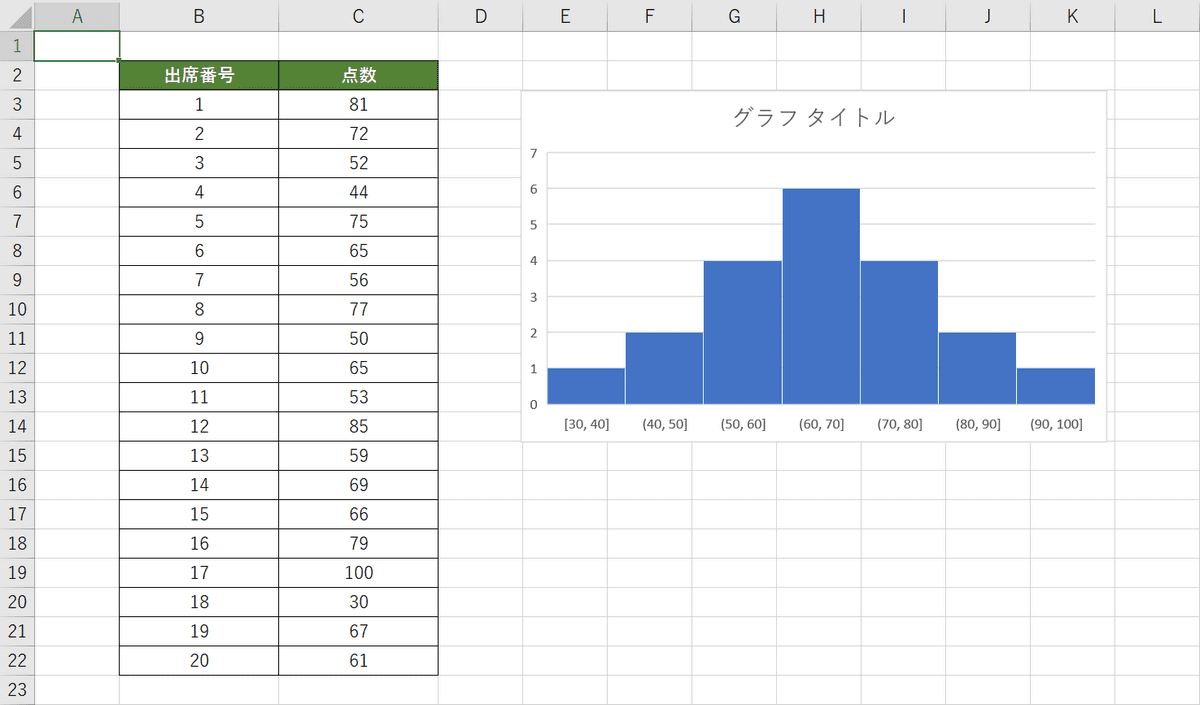


ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack


ヒストグラムからの標準偏差の求め方が分かりません 平均値をどう Yahoo 知恵袋



ヒストグラムから平均値 中央値を求める方法がわかりません 教えてください Clear



中学数学 中央値 メジアン の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



ヒストグラム Wikipedia



中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su



โน ตของ 数学 ヒストグラムでの平均値の出し方 ช น Junior Clear


ヒストグラム 度数分布表 とは Qc七つ道具エクセル ヒストグラム 度数分布表 作成の方法 図解 日本のものづくり 品質管理 生産管理 設備保全の解説 匠の知恵



子供向けぬりえ ベストヒストグラム 平均値 求め方



代表値 平均値 中央値 最頻値 の意味と違い 数学fun


平均値の求め方を教えてくださいお願いします 下のヒストグ Yahoo 知恵袋


代表値 平均値 中央値 最頻値 の意味と違い 数学fun
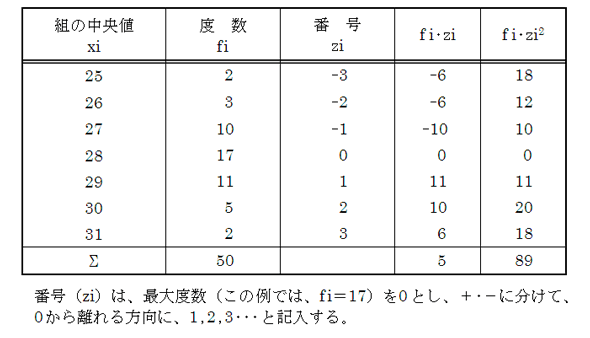


ヒストグラムの読み方 コツと経験則 実践 Ie 現場視点の品質管理 12 4 4 ページ Monoist



ヒストグラム Qcの世界 品質管理手法 Qc手法



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく


中学生の問題の平均値 中央値 最頻値の求め方教えて下さい 詳細の問題は画 Yahoo 知恵袋


3 2 平均 中央値 モードの関係 統計学の時間 統計web


度数分布表から標準偏差を求める 中卒でも分かる統計学入門 プログラマーを目指す 中卒 男のブログ


最頻値を求める 中学から数学だいすき


中1数学 資料の活用まとめ 用語の意味と求め方を徹底解説 数スタ


ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく


ヒストグラムから平均値を求める方法 全国 中学数学ができるようになるブログ
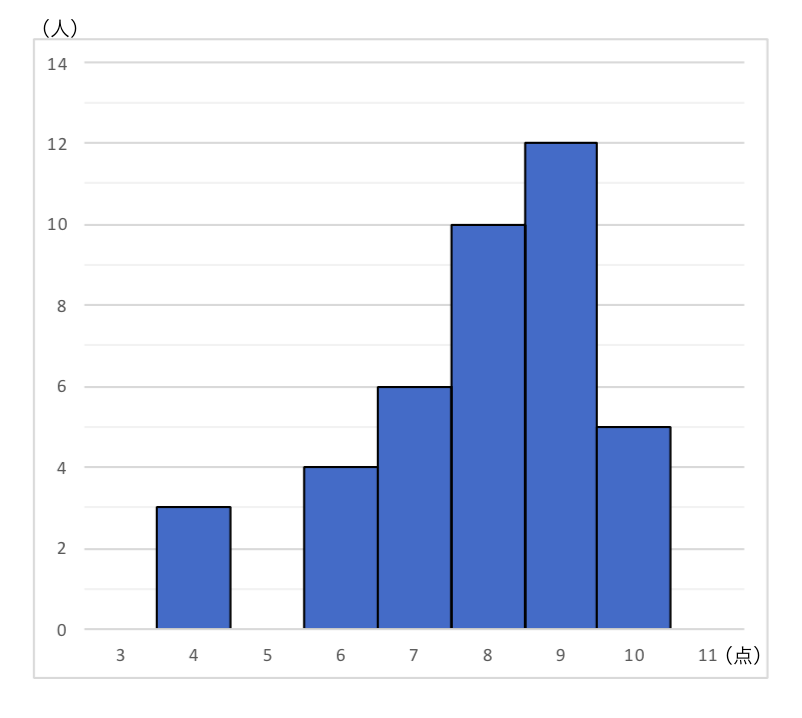


ヒストグラムから求める 平均値 中央値 最頻値 苦手な数学を簡単に
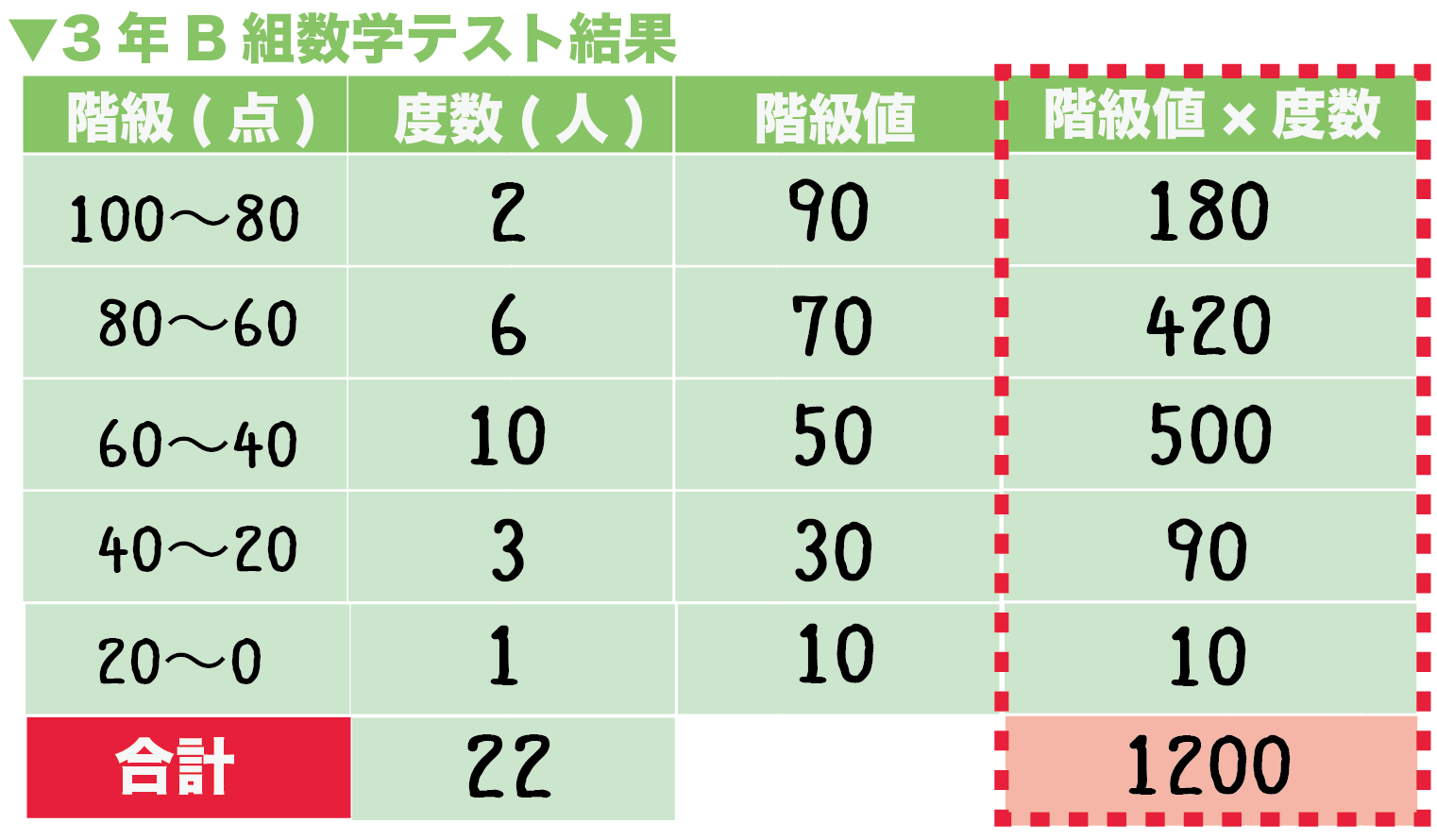


度数分布表からの平均値の求め方がわかる5ステップ Qikeru 学びを楽しくわかりやすく



小学6年生の算数 資料の調べ方 度数分布表 柱状グラフ 練習問題プリント ちびむすドリル 小学生



幹部社員 教育ポイント 経営改善ナビ
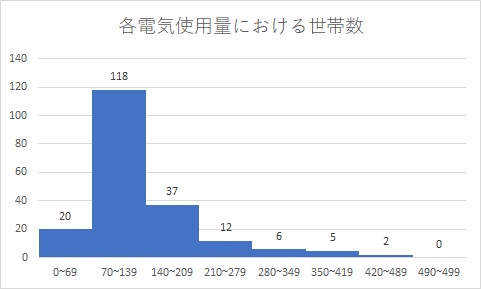


ヒストグラムから階級値を使って平均値と標準偏差を求めよう シグマアイ 仕事で使える統計を



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく



なるほど統計学園高等部 データの特性を見よう



中央値の求め方と最頻値の求め方を誰か教えて下さい よろしくお願いします Clear



数学における度数分布表とヒストグラムとは 中央値 最頻値も 高校生向け受験応援メディア 受験のミカタ
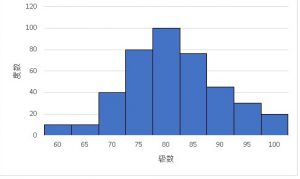


ヒストグラムから階級値を使って平均値と標準偏差を求めよう シグマアイ 仕事で使える統計を
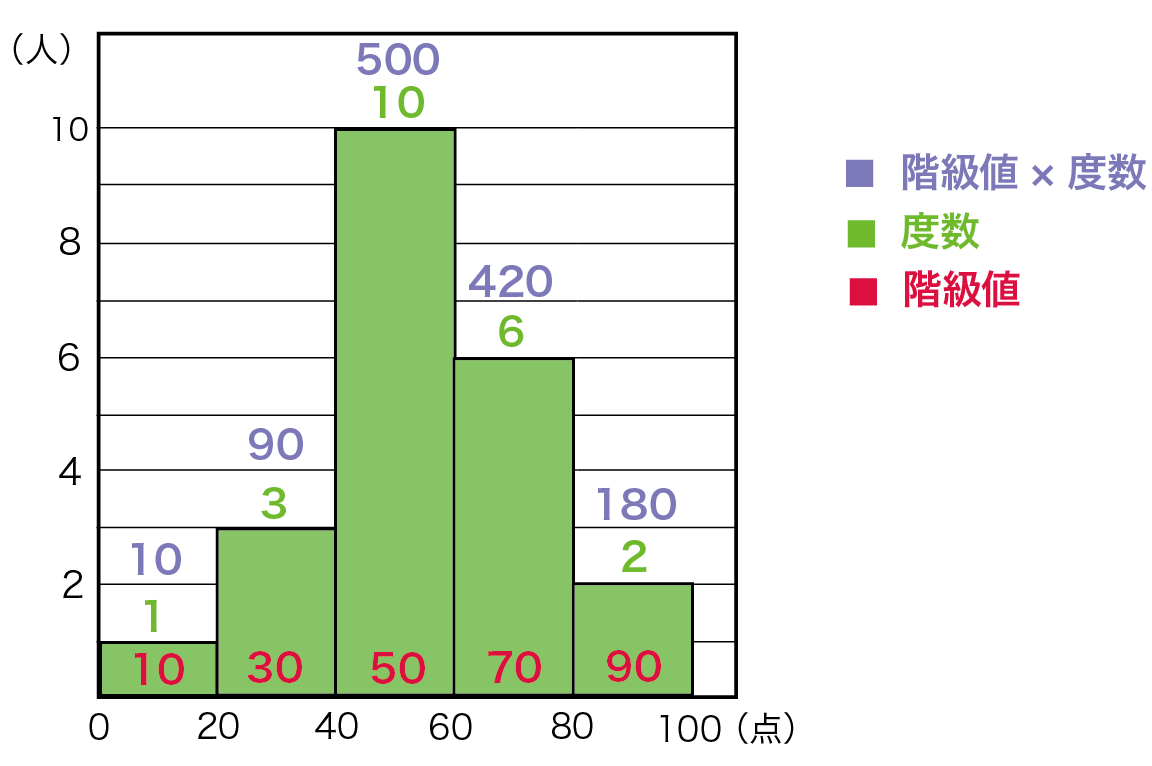


ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく


中央値とは 優しく図解 平均 代表値との関係 ふわっと理解 小学校の知識でわかる統計辞書



最も気に入った 資料の整理 中央値 デザイン文具
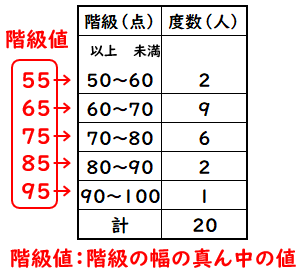


代表値 平均値 中央値 最頻値 の意味と違い 数学fun
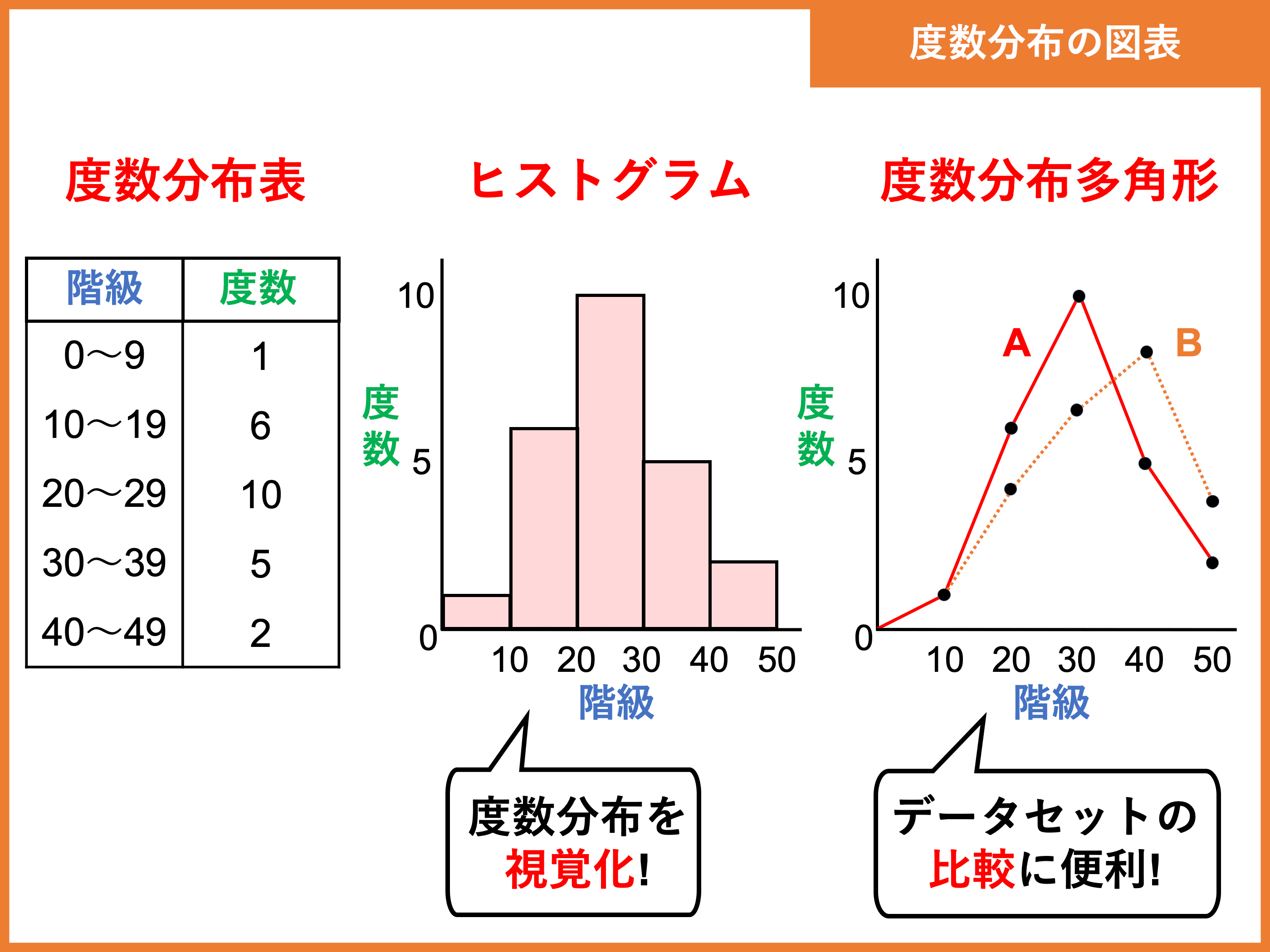


度数分布とは 表や多角形の作り方 平均値 中央値 最頻値の問題 受験辞典
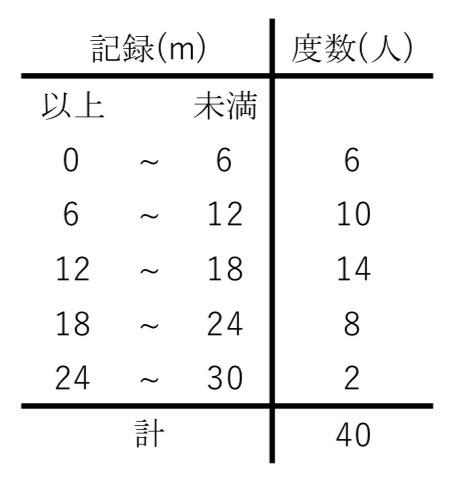


度数分布表から平均値と最頻値を求める 苦手な数学を簡単に



なるほど統計学園高等部 データの特性を見よう



高校数学 代表値 平均値と仮平均法 受験の月
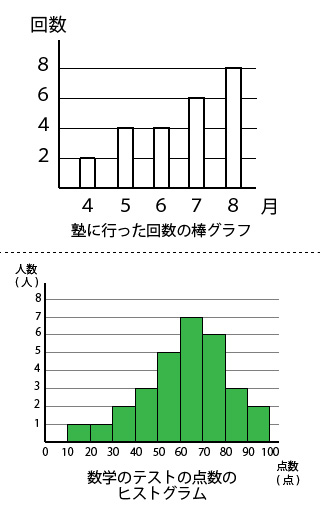


統計データの分析で使われる平均値 中央値 最頻値 もう一度やり直しの算数 数学


中1数学 中央値の求め方はこれでバッチリ 偶数 奇数の場合をそれぞれ解説 数スタ
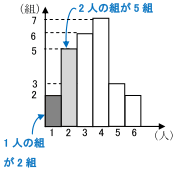


ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション



分布の中心 分布の中心を表す要約統計量には平均値 中央値 最頻値がある


テクノビジョン ダイジェスト
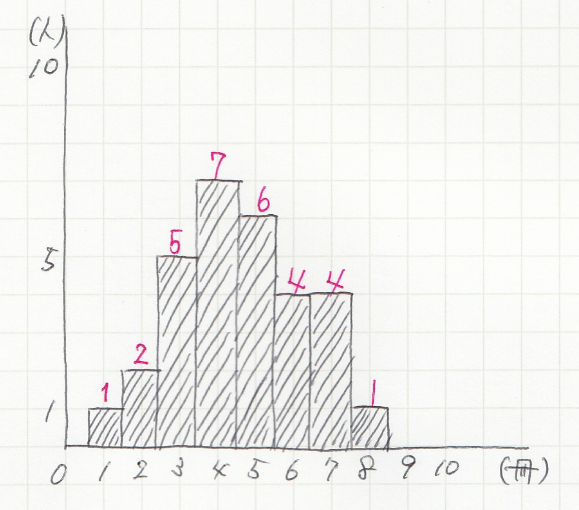


ヒストグラムから平均値を求める方法 全国 中学数学ができるようになるブログ
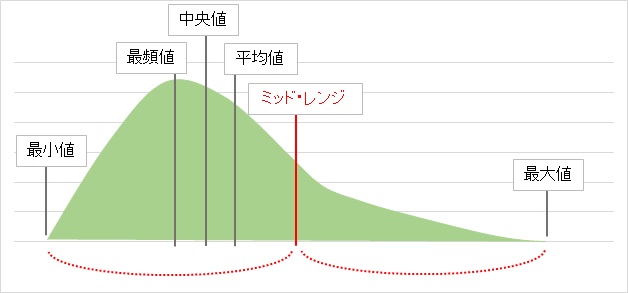


ミッドレンジの意味と計算 統計学 統計学が わかった


ヒストグラムの平均値の求め方教えて下さい ヒストグラムから Yahoo 知恵袋
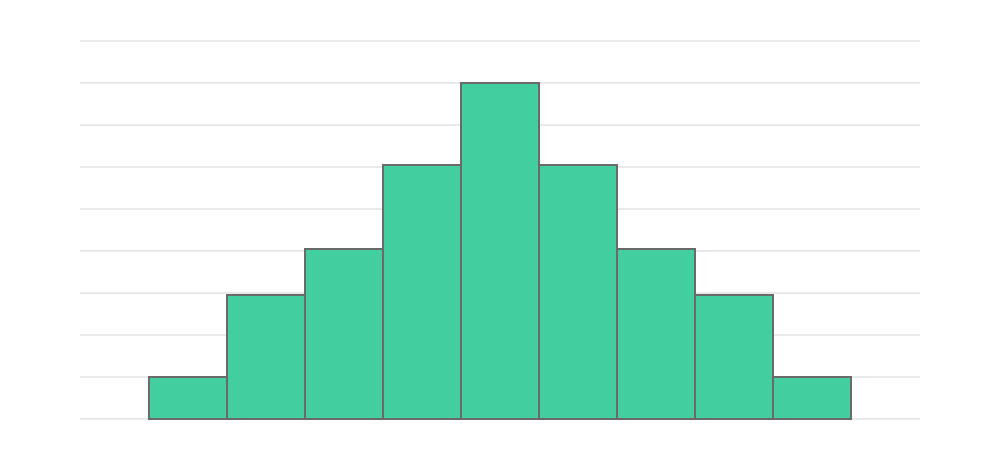


ヒストグラムとは ヒストグラムの書き方 作り方 や分布図の見方を徹底解説 Backlogブログ
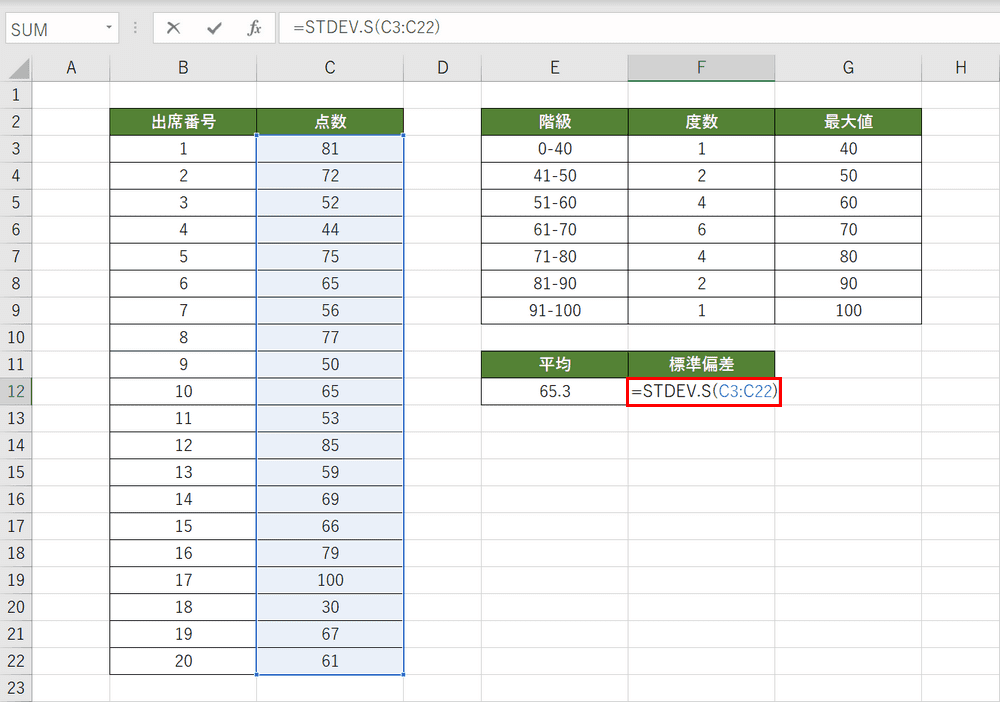


ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack
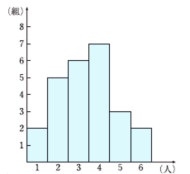


ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション


32 1 外れ値 統計学の時間 統計web


分布 平均 分散 しまね統計情報データベース
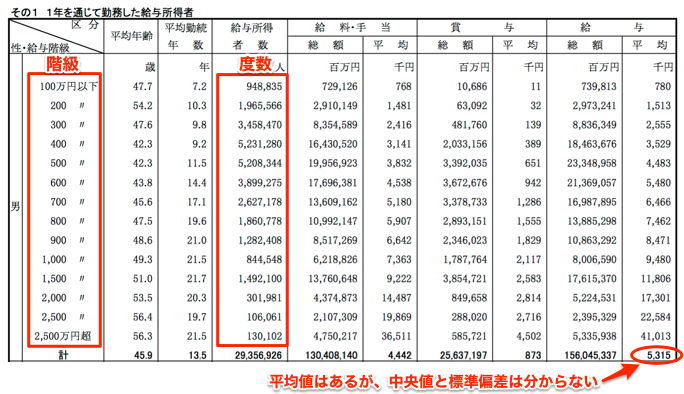


度数分布表からpythonで平均値 中央値 標準偏差を推定する方法 ガンマソフト株式会社



ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく


3 2 平均 中央値 モードの関係 統計学の時間 統計web
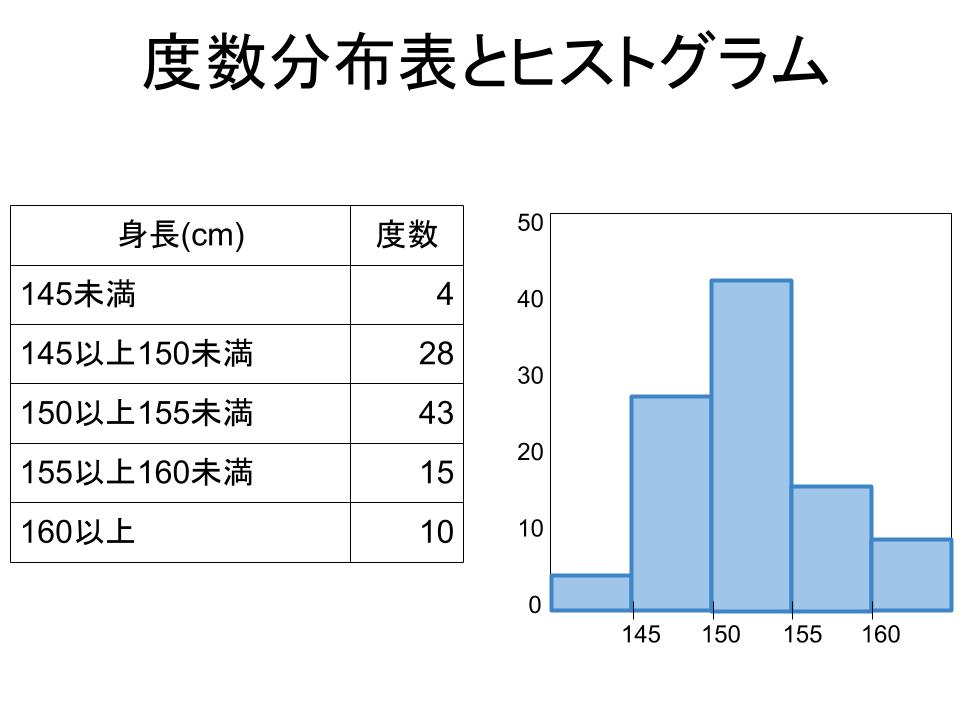


経営を学ぶ 経営学 Mba 起業
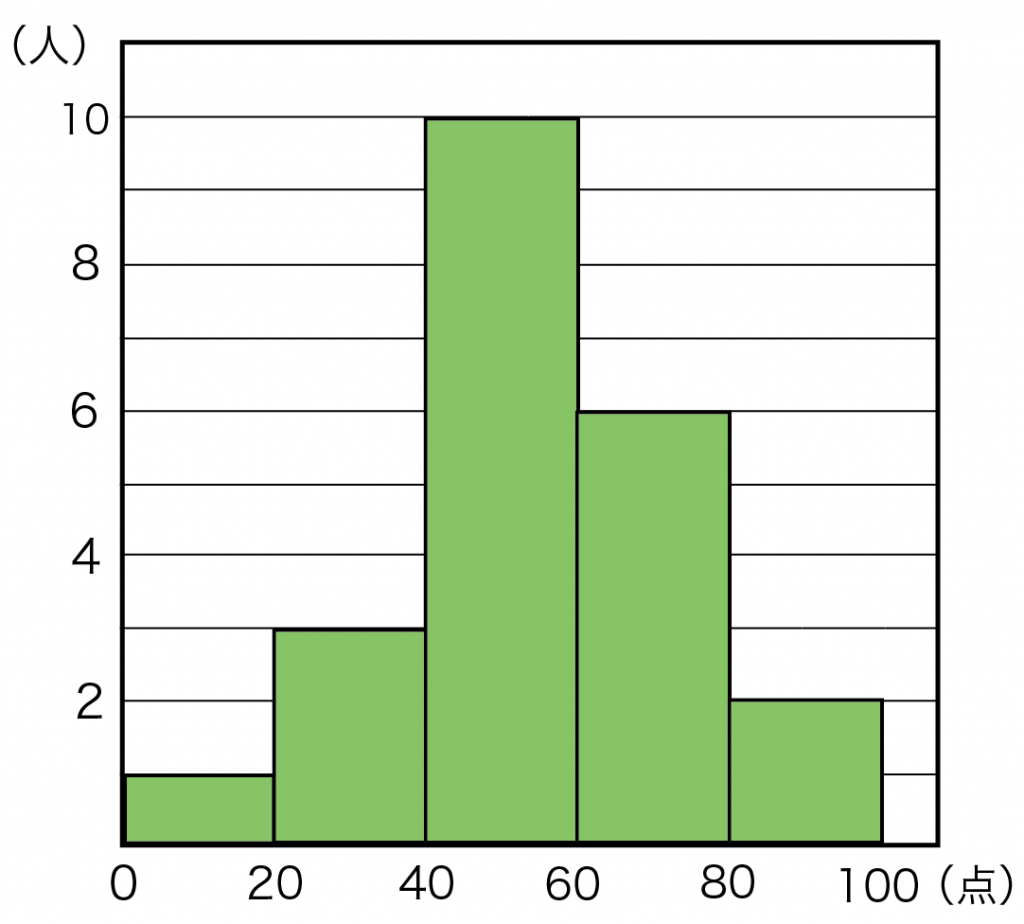


ヒストグラムを使った平均値の求め方がわかる4ステップ Qikeru 学びを楽しくわかりやすく
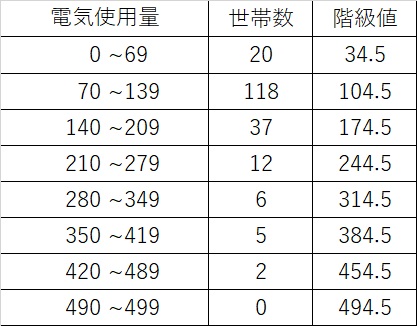


ヒストグラムから階級値を使って平均値と標準偏差を求めよう シグマアイ 仕事で使える統計を


ヒストグラムが与えられたデータから 中央値を求める方法 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション
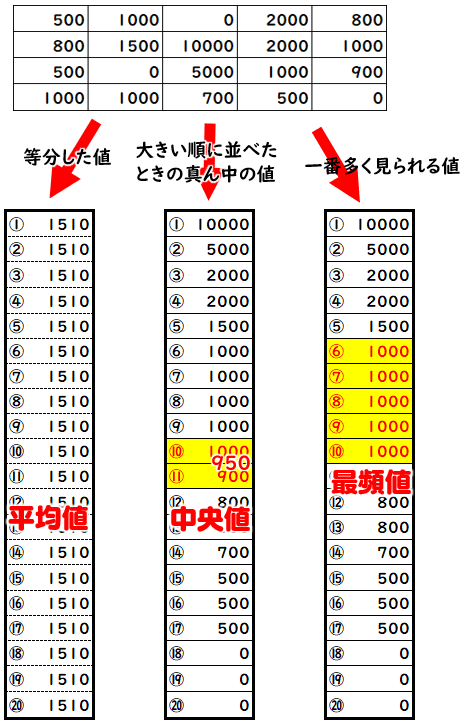


代表値 平均値 中央値 最頻値 の意味と違い 数学fun
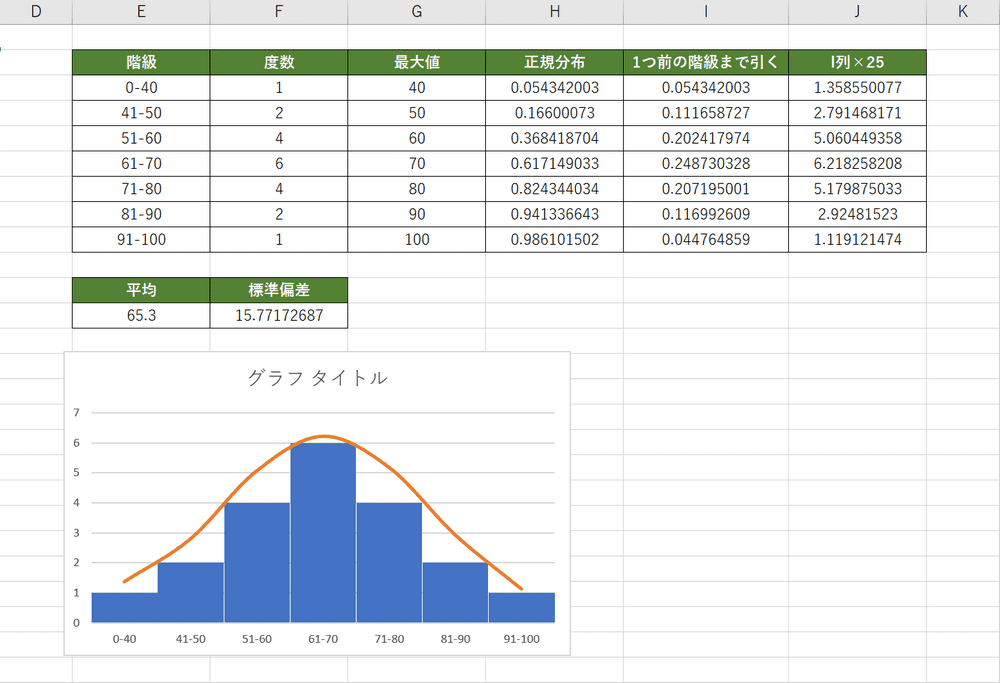


ヒストグラムとは エクセルによるヒストグラムの作り方 書き方 Office Hack
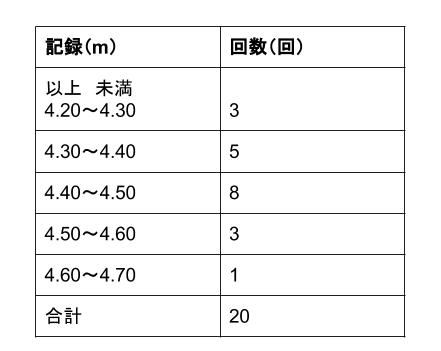


中学数学 代表値 中央値 中学数学の無料オンライン学習サイトchu Su
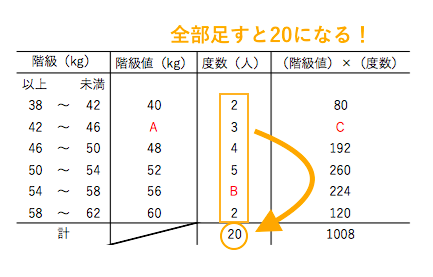


平均値と階級値について 苦手な数学を簡単に
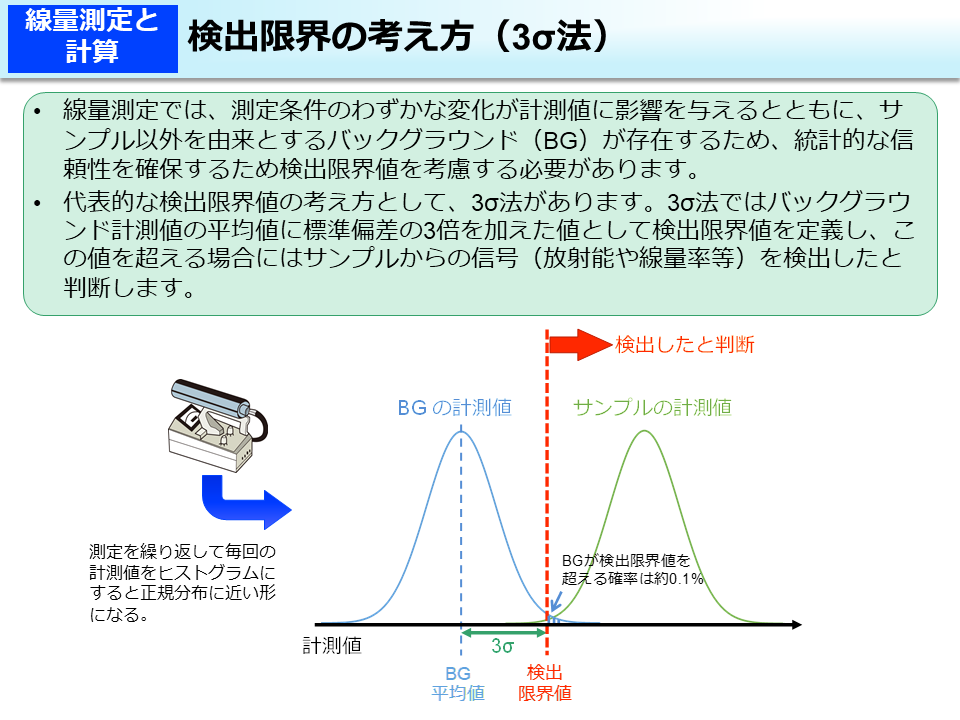


環境省 検出限界の考え方 3s法



最新ヒストグラム 平均値 求め方 ただぬりえ



0 件のコメント:
コメントを投稿